Bayes for Beginners
Bayesian statistics have a reputation in occupational hygiene for being overly complex. While it’s often impossible to calculate an answer by hand, the Bayes’ ideas are simple and intuitive. I’d like to try to convince you that not only can you use Bayesian statistics as a hygienist, you should!
Baye’s Theorem is a simple one. Take what you already know and combine that with new evidence you collect. You now have an updated, and more informed position.
That’s literally it.*
Below are two examples to help demonstrate this idea. The first is (hopefully) intuitive with no math, and the second includes some basic numbers.
Example 1 - Intuitive
Let’s say you woke up one morning and stepped outside to grab the newspaper. To your surprise you found it lying on the footpath, soaking wet! That’s a first… you wonder what could have happened. You think of possible causes. Maybe there was a rain shower, maybe your neighbour had their sprinklers on too high, maybe an underground pipe burst, or someone spilt their morning coffee.
We don’t know for sure, but we can make some reasonable predictions. Rain and a rouge sprinkler are decent guesses, a burst pipe seems pretty darn unlikely. If we where to graph how likely we think each cause is, it might look like this:
Prior beliefs about what caused the wet newspaper
This is the probability of the potential causes “you” believe caused the wet paper before you’ve collected any additional information. Of course, you might have a different opinion. Any opinion is fine, as long as you can justify it!
What if you were then to look around and see that the ground, and everything else as far as the eye could see, was wet too? How would this new information affect your beliefs? Rain is now by far the most reasonable explanation. Consequently, the other opinions must be impossible (or at least extremely unlikely).
Updated beliefs after seeing water everywhere
Alternatively, what if you noticed a bright sunny morning, a discarded coffee cup, and a small brown puddle? You could argue the burst pipe increased in probability (eww). That’s still not too likely. The best money is on a careless pedestrian.
Updated beliefs after seeing coffee cup and small puddle
This is all Bayesian statistics is. We are just updating an exisiting belief with new information. Simple. However, our information isn’t typically so demonstrative. Instead each piece of new evidence (like an exposure sample) shapes our beliefs step-wise.
Now that you’re warmed up, let’s do an example with numbers.
Example 2 - Mathematical
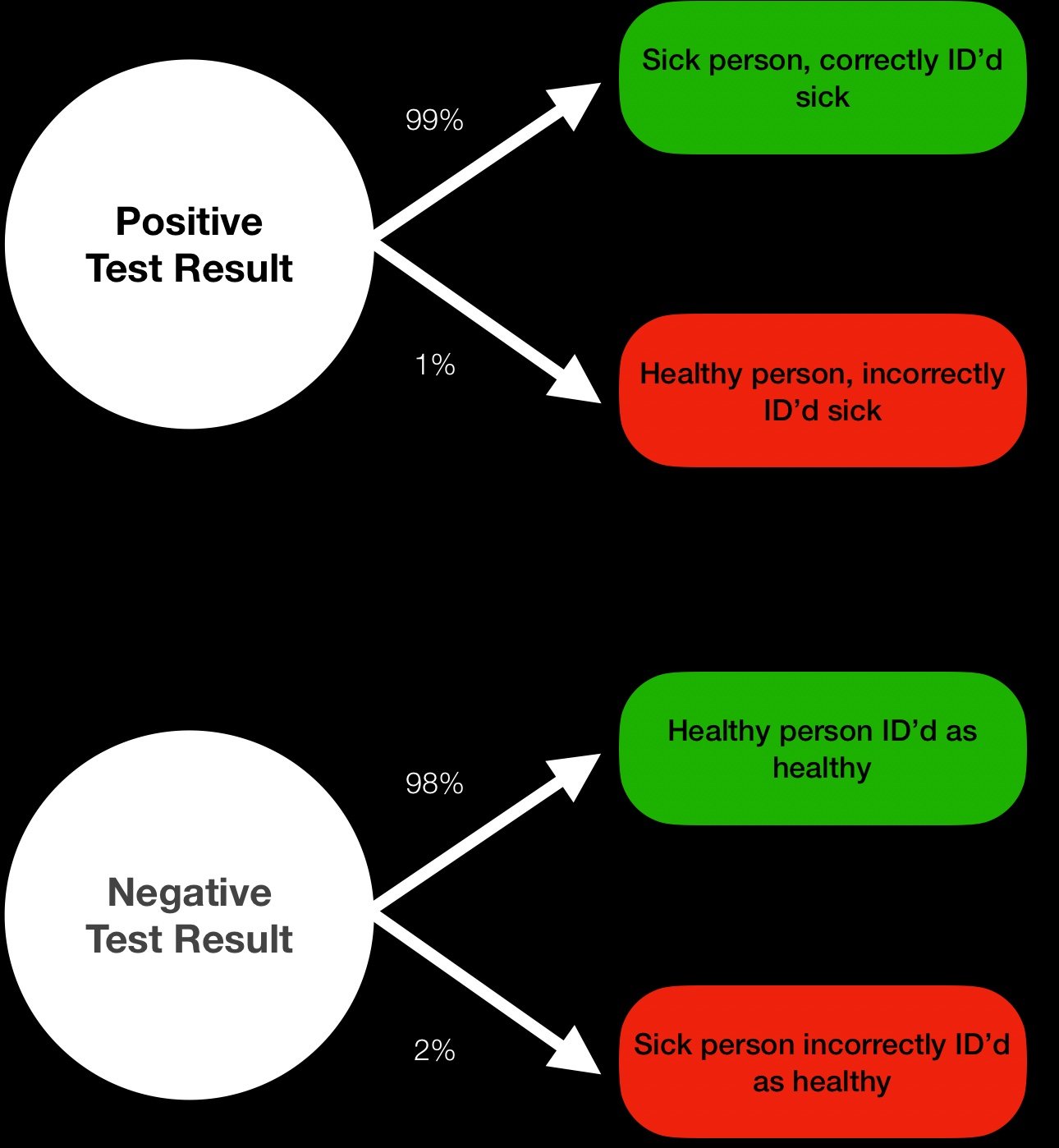
You’re an occupational physician doing Hepatitis B screening tests for aged care workers. The test you administer can correctly identify positive cases of Hep B 99% of the time. The test only incorrectly diagnoses sick people as healthy 2% of the time. Seems pretty reliable!
If a worker tested positive, you can 99% confident that they actually have Hepatitis B.
Screening test accuracy
Let’s say you have access to an extensive database and know that Hep B occurs in about 0.8% of aged care workers. Does this change your belief about the reliability of a positive result?
Stop here for a think.
The company you are working for has 6,500 workers around the country. You expect about 52 cases of Hep B (0.8 %).
After testing everyone, you expect 51 correct positive results (52 cases * 99% accuracy). You’d also expect 129 health people with incorrect positive results (6,448 healthy people * 2% false positive rate).
So we have 180 total positive tests, of which 51 are actually correct. Oh dear. If a worker had a positive test result, there’s only 28% chance that they actually have Hepatitis. Much less confident than our original 99%.
Of course, you can incorporate more information (I.e. conduct a second test) and update your position again. For those curious, a second positive test would give ~94% confidence of Hep B.
See how impactful incorporating exisiting information can be?
Application to Occupational Hygiene
Hopefully you are already imagining all the ways that Bayesian statistics can be used in occupational hygiene. A few clarifications may help:
What can you used to create a prior?
Anything! You could use:
results you have already collected,
data from industry,
data from literature,
exposure modelling data,
professional judgement.
Just think “could I convince a skeptic that this prior is appropriate?”.
How do you calculate something that “can’t be calculated by hand”?
A Monte Carlo Markov Chain. A topic which deserves its own post.
How often should I be updating my belief in practice?
As often as you like! There are no rules. This is why Bayes’ Theorem is so useful in occupational hygiene - very rarely (if ever) do have a mountain of conclusive data. Instead we collect data piece-by-piece, and our position can likewise change as the information comes to hand.
How do I actually use Bayesian statistics in my exposure monitoring program?
The easiest way to get started is to use existing tools like ExpoStats or IHStat_Bayes. They are both free and easy to use, but you can’t easily customise the prior.
IH_DataAnalyst allows for prior modification within the AIHA decision making matrix.
To have full control over your priors, you will need to learn some statistics and programming. Again, beyond the scope of this post.
Conclusion
Bayesian statistics is just a fancy way of updating our beliefs with new evidence. You probably already know a lot about the exposure scenario before you start monitoring. This prior knowledge shouldn’t be lost when conducting a monitoring campaign. Hopefully you can see that it’s not as intimidating as it may first appear. It’s like it was designed specifically for occupational hygienists. So please, have a play. It’s worth your time, believe me :)
Footnote:
* Ok, yes, the formula is very slightly more complex. But not by much. And this is essentially what’s happening at its core.
References:
Kruschke, J. (2014). Doing Bayesian Data Analysis. Edition 2.
Motulsky, H. (2018). Intuitive Biostatistics: A non mathematical guide to statistical thinking. Edition 4.
Fun Youtube videos on the topic:
https://www.youtube.com/watch?v=7GgLSnQ48os
https://www.youtube.com/watch?v=HZGCoVF3YvM
https://www.youtube.com/watch?v=R13BD8qKeTg